Difference Between Divergence and Curl in Vector Calculus

Intro: If you’ve ever sat through a physics class and wondered why these two operations keep popping up, you’re not alone. Divergence and curl are like two ways to describe the direction and intensity of a flow in a field. They look similar on the page but tell very different stories about how a vector field behaves in space—and those stories translate surprisingly well to how we think about markets, risk, and trading dynamics on the desk.

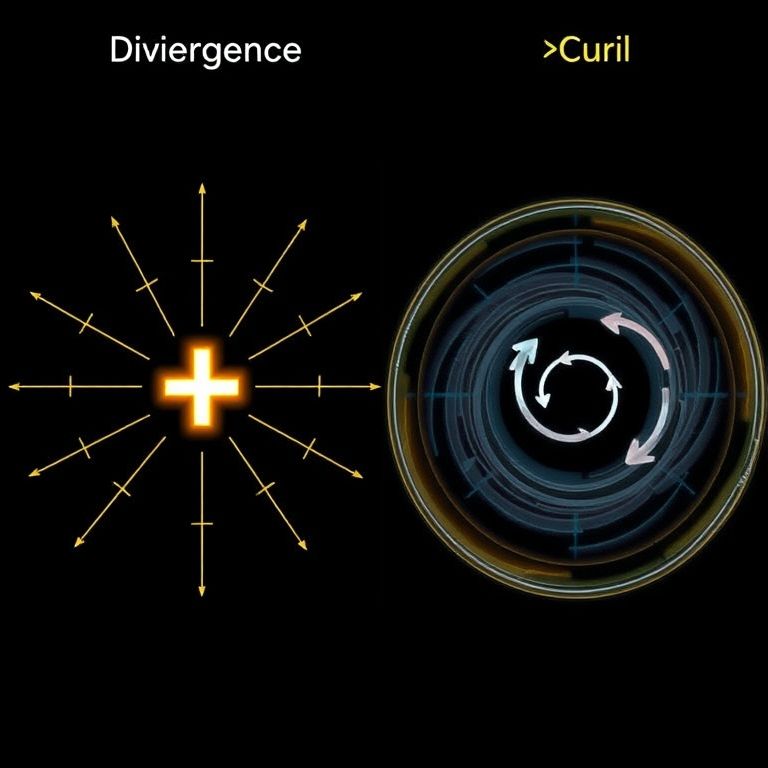
Divergence: what it tells you

• The core idea: Divergence measures how much a point acts as a source or sink for the field. It answers “is there net outflow or inflow at this location?” (mathematically, ∇·F).
• Geometric intuition: If the arrows around a point tend to point outward, the divergence is positive; inward arrows signal negative divergence. It’s like counting how much the fluid is being created or absorbed locally.
• Everyday example: In a simple flow, a source pushes flow outward, while a sink pulls it inward. In weather maps, positive divergence can hint at rising air and potentially storm development.

Curl: what it tells you

• The core idea: Curl captures rotation. It answers “how much is the field swirling around this point?” (mathematically, ∇×F).
• Geometric intuition: Curl measures local rotation or swirl. A zero curl means no local spinning, while a nonzero curl indicates a vortex-like motion with a definite axis direction given by the right-hand rule.
• Everyday example: Whirlpool-like motion in fluids or the rotating wind around a low-pressure system.

Key differences at a glance

• Scalar vs vector: Divergence yields a scalar field; curl yields a vector field.
• Flux vs rotation: Divergence tracks net flux density, curl tracks rotation density.
• Theorems in play: Gauss’s divergence theorem connects divergence to outward flux, while Stokes’ theorem ties curl to circulation along a boundary.

Trading and modeling analogies

• A mental model for markets: think of the price field as a vector landscape. Divergence is like local supply/demand “sources” that push prices away from equilibrium; curl resembles momentum or rotational effects as prices swing around a level.
• Practical cautions: markets aren’t smooth vector fields. Real data are noisy, and you’re rarely measuring a perfect continuum. Use divergence and curl as intuition builders in risk surfaces or heatmaps, not as exact predictors.

Mult Asset learning and strategies

• Across forex, stock, crypto, indices, options, commodities: the same ideas help you map where liquidity concentrates (low divergence) or where order flow spins (high curl). When you combine across assets, you notice if a cross-asset regime change shows up as a shift in the field’s divergence pattern or a new curl swirl in volatility surfaces.
• Reliability tips: backtest on synthetic fields, stress-test under regime shifts, and fuse these ideas with flow-based indicators and order-book signals. Don’t rely on a single metric; use a composite view with proper risk controls.

DeFi, AI, and prop trading outlook

• DeFi realities: decentralized finance brings new liquidity layers and smart contracts, but liquidity fragmentation and oracle risk create measurement noise in any “field” you model. Expect more cross-chain data challenges and front-running risks.
• Smart contracts and AI-driven trading: smart contracts open programmable market microstructures; AI can detect changing divergence and curl patterns faster than humans, provided data quality is solid and you guard against overfitting.
• Prop trading growth: multi-asset desks benefit from a geometric view of flow—divergence helps spot expanding liquidity pockets; curl helps spot turning momentum. The future lies in integrated models that combine vector-field intuition with robust risk controls and cross-asset correlation analysis.

Slogans to keep handy

• Divergence tells you where the market is sprouting; curl tells you where momentum swirls.
• Read the flow, not just the price—where sources rise, where rotations form, and trade with the current.
• Flow-aware trading: from DeFi to AI, the geometry of markets guides better risk-aware decisions.

Wrapping up: the difference between divergence and curl isn’t just Math 101—it’s a lens for understanding how markets evolve. Used wisely, it informs risk limits, strategy design, and even on-chain trading ideas as the crypto and DeFi worlds mature.

YOU MAY ALSO LIKE